Centro Regional De Educación Normal Dr. Gonzalo Aguirre Beltrán.

Blvd. Manuel Maples Arce s/n Ejido La Calzada, C.P. 92880
Telefonos: 783 8370593 - 783 8370126

Unidad 4
Desarrollo del razonamiento proporcional

Razon y Proporción
Competencias de la unidad de aprendizaje
• Distingue las características de las propuestas teóricas metodológicas para la enseñanza de la aritmética en la escuela primaria para aplicarlas críticamente en su práctica profesional.
• Identifica los principales obstáculos que se presentan en la enseñanza y el aprendizaje de la aritmética en la escuela primaria y aplica este conocimiento en el diseño de ambientes de aprendizaje.
• Relaciona los saberes aritméticos formales con los contenidos del eje sentido numérico y pensamiento algebraico del plan y programas de estudios de educación primaria para diseñar ambientes de aprendizaje.
• Emplea la evaluación como un instrumento para mejorar los niveles de desempeño de los alumnos de la escuela primaria en la resolución de problemas.
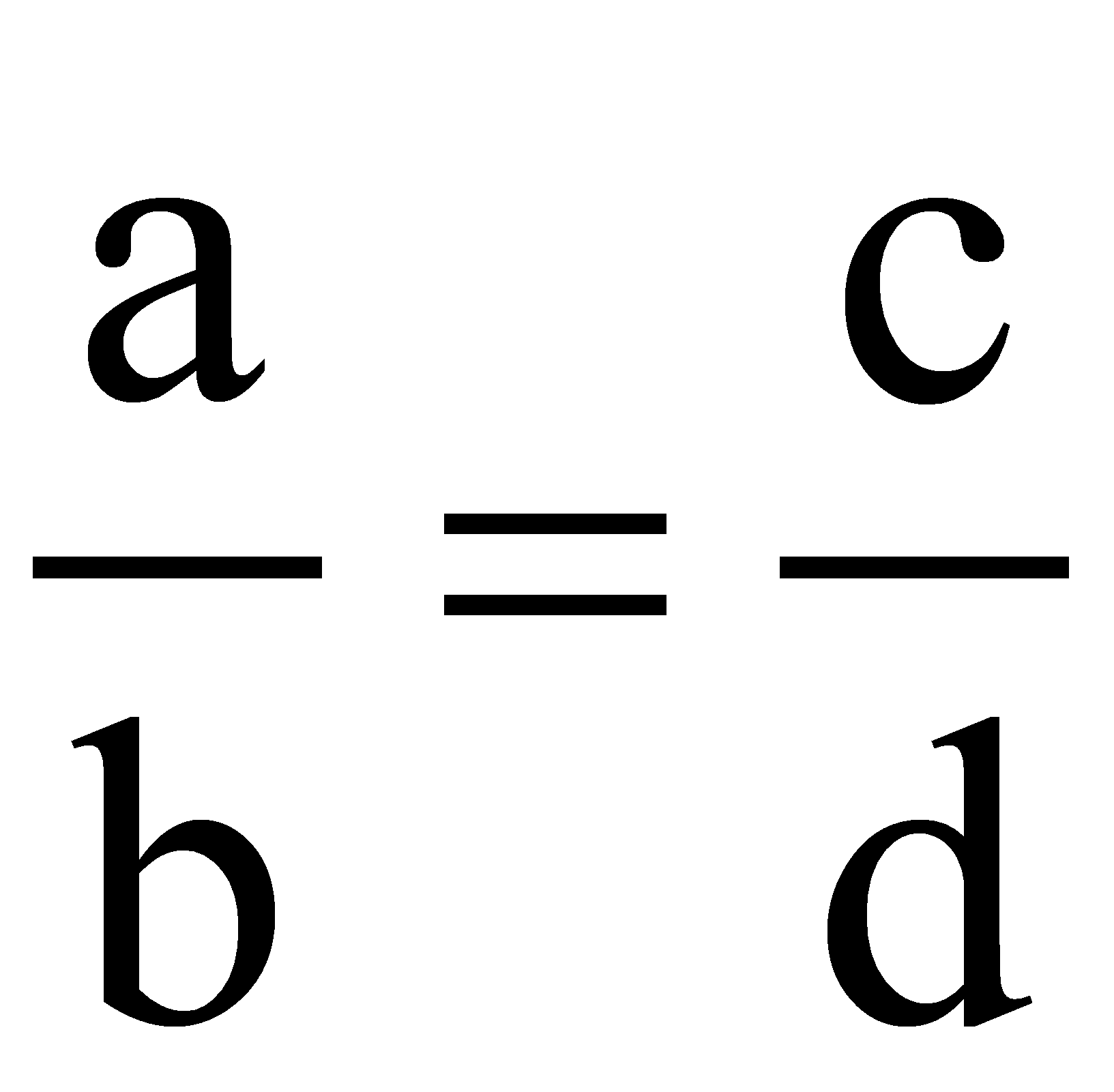
RAZÓN
Razón o Relación de dos cantidades es el resultado de comparar dos cantidades.
Dicha comparación podría indicarse como una razón, en cuatro formas distintas, de este modo:
1.- a:b
2.- a ÷ b
3.-
4.- La razón de a es a b.
En una razón A/B al primer término (A) se le llama antecedente y al segundo (B) se llama consecuente.
Ejemplo de Razon
En una clase de un colegio cada pelota es utilizada por cada cinco niños, o sea que tenemos cinco veces más alumnos que pelotas de fútbol. Tenemos entonces en este ejemplo de razón que la relación entre alumnos – pelotas es 5 a 1. Esta razón se denota 5/1 y la podemos leer como: cinco es a uno. El valor de la razón la obtenemos dividiendo 5/1=5. Concluimos con este ejemplo de razón que existe el quíntuple de alumnos que de pelotas de fútbol.
Proporción
La proporción muestra los tamaños relativos de dos o más valores.
Las proporciones pueden mostrarse de diferentes maneras. Usando el ":" para separar los valores, o como un solo número dividiendo un valor para el total.
Una proporción se puede escribir de diferentes maneras:
-
3:1 Usando un ":" para separar valores de muestra
-
¾ en fracción, dividiendo un valor entre el total (3 de cada 4 cajas son azules)
-
0,75 en decimal
75%en porcentaje
Proporcionalidad
Muchas veces en la práctica se nos presentan situaciones en las que el valor o cantidad de una magnitud depende del valor de la otra.
Por ejemplo, si un metro de tela tiene un precio de $ 10, el costo de un corte de tela depende del número de metros que tenga el largo. A mayor número de metros de tela corresponde un mayor costo.
Proporcionalidad directa
Cuando dos magnitudes están relacionadas de modo que los valores de una de ellas se obtienen multiplicando por un mismo número los valores correspondientes en la otra, se dice que son directamente proporcionales
En el ejemplo de los metros de tela, el costo del corte de tela se obtiene multiplicando la longitud del corte por el precio de un metro que es $ 10. Podemos decir entonces que el costo de una tela es directamente proporcional a la longitud del corte. El número por el que se multiplica se llama factor de proporcionalidad. En este caso es 10 ese factor.
En una proporcionalidad directa dos cantidades cualesquiera de una magnitud y sus correspondientes en la otra forman una proporción.
Ejemplo: si hay un niño y tres niñas puedes escribir la proporción así:
1:3 (por cada niño hay tres niñas)
1/4 son niños y 3/4 son niñas
0,25 son niños (dividiendo 1 entre 4)
25% son niños (0,25 en porcentaje)

Porcentaje
El pocentaje nos dice qué parte de un total representa una cantidad. Y lo hace representando el total por el valor 100 y calculando de esos 100 cuanto correspondería a la cantidad que estamos analizando.
Por ejemplo:
Si hay 10 coches aparcados y 3 son de colo amarillo, ¿Qué porcentaje (que parte del total) representan estos 3 coches?
El total (los 10 coches aparcados) se considera que es el 100 por cien (se representa por 100 %).
Para calcular el porcentaje que representan los 3 coches amarillos:
Se divide el número de cohes amarillos entre el total de coches y se multiplica por 100 (para expresarlo en porcentaje):
3 : 10 = 0,3
0,3 x 100 = 30 %
Los 3 coches amarillos representan el 30% de los coches aparcados.
Veamos otros ejemplos:
En una familia de 6 hermanos 4 son rubios ¿Qué porcentaje representan del total de los hermanos?
4 : 6 = 0,666
0,66 x 100 = 66,6 %
Un equipo ha jugado 15 partidos y ha ganado 6 ¿Qué porcentaje representan los partidos ganados sobre el total
6 : 15 = 0,4
0,4 x 100 = 40%
En qué consiste la regla de tres
La regla de tres es una regla matemática que permite resolver problemas basándose en la proporcionalidad. Mediante la regla de tres puedes obtener un número que desconoces basándote en la proporción existe entre dos números que si conoces y un tercer número del que quieres sacar la relación proporcional. Esto se expresa de la siAaguiente forma:
Tengo dos valores relacionados A y B, un valor de referencia X y quiero obtener el valor de Y. La regla de tres me indica que B es en relación a A, lo que Y es en relación a X.
Glosario
Lúdico:Todo aquello propio o relativo al juego, a la diversión.
Pagina: http://www.definicionabc.com/social/ludico.php
Didactica: Es el campo disciplinar de la pedagogía que se ocupa de la sistematización e integración de los aspectos teóricos metodológicos del proceso de comunicación que tiene como propósito el enriquecimiento en la evolución del sujeto implicado en este proceso.
Pagina web: http://definicion.de/didactica/
Algoritmo: Método para resolver un problema mediante una secuencia de pasos a seguir. Dicha secuencia puede ser expresada en forma de diagrama de flujo con el fin de seguirlo de forma más sencilla.
Pagina Web: http://candyluna.galeon.com/aficiones813476.html
Constructivismo: Es el modelo que mantiene que una persona, tanto en los aspectos cognitivos, sociales y afectivos del comportamiento, no es un mero producto del ambiente ni un simple resultado de sus disposiciones internas, sino una construcción propia que se va produciendo día a día como resultado de la interacción de estos dos factores.
Pagina Web: http://www.monografias.com/trabajos11/constru/constru.shtml
Andamiaje: Planteamiento del aprendizaje concebido como una construcción colectiva donde los aprendientes construyen su propio conocimiento y comprensión de la lengua.
Pagina Web: http://cvc.cervantes.es/ensenanza/biblioteca_ele/diccio_ele/diccionario/andamiaje.htm
